Previously [1, 2, 3], I've talked about the effects of what I call the "reinterpretation problem". This effect, known also as the havoc effect, is characterised by a reinterpretation of input segments as a result of a mutation. Think of a sequence of network packets, each with a length field: if you mutate one of the length fields, the remaining sequence of packets will be interpreted another way -- that is, unless you take special care to preserve them [4].

But there is more to reinterpretation than the base-level effects of length fields and type flags. The program itself often reinterprets our inputs in subtle ways. Recently, I created an exercise to help people learn how to use LibAFL [5]. This was built around using a fuzzer to solve "Rush Hour" (or, "Tokyo Parking") puzzles [6], and is my second foray into fuzzing puzzles [7]. I enjoy building fuzzers for such problems because they really exercise the limits of fuzzer capabilities; one cannot simply rely on havoc mutators [8]. But, simply implementing a different mutation strategy can be enough to beat all the sample puzzles I provided in the exercise; everything past that is simply unnecessary optimization. So, what characterises this "program" as fuzzable under one mutator, but not another, when both mutators preserve the syntactic correctness of the input?

The answer is, as always: the reinterpretation problem. Or, at least, that's the first part. :)

A deeper analysis of fuzzing parking problems

In "Tokyo Parking" [6], cars are arranged on a grid. They are forced to travel in a particular orientation (up/down or left/right) and may only move in a given direction when there are no obstacles. The goal is to get the "objective" vehicle to the right wall (and therefore "leave" the parking lot).

This is not something you need to fuzz to solve. Reencoding the problem as a state machine, one can simply BFS your way to victory. In fact, the final state of the exercise is just this: getting to a point where your fuzzer is so adept at snapshot fuzzing and determining which mutations are even viable that you, effectively, are just doing breadth-first search. The purpose of the exercise is to guide students to understanding that fuzzers are merely search algorithms, albeit very nondeterministic ones with not a whole lot of insight into the search space.

Getting back on track: the critical part of fuzzing parking puzzles is that the input itself represents a sequence of moves. The input is then "executed" by moving the cars on the board accordingly, and the "program" (i.e. the map) "crashes" when the car runs into something. In other words, the executor terminates early if a move cannot be reconciled with the state of the board.

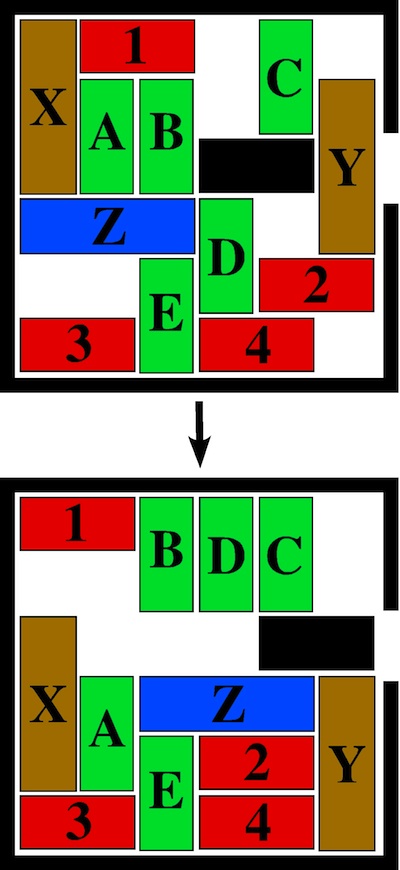
The first mutator that the students implement mutates move sequences by inserting a random move at a random index. This is enough to solve the first puzzle, but not nearly strong enough to solve the last in a reasonable time. The reason for this difference in performance is simple: inserting a random move at a random position is likely to fail. If we consider this at the move level, there are some fairly obvious reasons for this: the move is randomly generated and thus may disregard orientation rules, and inserting at a random position means that the move, even if valid for that car, is likely to fail because the car will encounter an obstacle in that direction. This is especially true for puzzles with dense populations of cars. Below is map 36 from Tokyo Parking in its starting and final states as provided by Jim Storer [9]:

This is a very tight grid of cars, which causes most moves to fail outright. Students are instructed in the exercise to build a measurement tool to determine the failure rate of inputs being executed. With the random insertion mutator, the failure rate on this puzzle is approximately 98% and takes about 5.6 seconds to complete a solve on my machine.

Curiously, we can improve performance with a very trivial change. If we modify the mutator to only append these moves (with no other cleverness), the failure rate drops to 88% and the puzzle is solved in 0.17 seconds. A remarkable improvement for so simple a change, and without snapshotting!

The reason for this is simple: when we insert moves, even if they are valid at that point, we invariably change the state of the puzzle. This causes subsequent moves to suddenly fail due to encountering obstacles.

Sound familiar?

Thinking about input shapes

If you have the (mis)fortune of working with people who think about fuzzing all day, you will likely hear the phrase "input shape" thrown around. While typically this refers to how the program under test actually interprets the input (e.g., "the input shape is a JSON document"), we can reason about these shapes more generally than just specific inputs.

I propose that there are two types of inputs: instruction-like and data-like. Of course, there is some overlap where, for example, an instruction contains data, or data contains instructions, but fundamentally, this is what inputs are consumed as by the program. For both of these types, you have three shapes: linear, tree, and directed graph.

Linear inputs

The parking game example from above is an example of a linear input. The input can be delineated into meaningful segments which happen in an exact order unconditionally. Other examples may be things like sequences of system calls [10] or network packets [11].

This input shape is most suitable for snapshot fuzzing. Generally, the harness will consume the linear sequence in some loop surrounded by setup and teardown routines. Splitting up the harness allows you to snapshot at the boundaries of the input segments. Then, using your stashed state, you may continue with a variety of different subsequent input segments without having to start from the beginning again.

This input shape is also interesting from a theoretical perspective: we can distinguish states of the target based on its behavior when presented with the same input segment with different preceding input segments. Consider the parking game fuzzer again: without being able to observe the actual game board, we can check if two different states are the same by checking whether the same moves are possible for each. Given enough time, we could even infer the whole state of the game board based on this strategy. This feature makes linear inputs quite interesting from a fuzzing perspective, especially as it comes to finding guidance beyond edge coverage -- but we'll get to that later.

Tree inputs

Structurally, tree-shaped inputs are fairly similar to linear inputs, but without the same guarantees about how the program utilises it. These inputs are generally consumed at a token level and then parsed into some greater structure -- then something is done with that greater structure. In this way, it is more difficult to fuzz in a snapshotting manner.

This input shape is relevant for human-readable inputs, and generally only for inputs which are not self-referential (e.g., JSON). If we begin to consider the relationship between branches in this tree (e.g., variable definition and use), then it would be more considered like the inputs in the next section.

Like linear inputs, tree-shaped inputs have features which enable smarter fuzzing, too. Because the code regions which correspond to various parsing routines can be distinguished, one can infer the types of subtrees that correspond to different input segments. In this way, we can implement crossover and mutation operations which are more likely to preserve syntactic correctness. Also, there's always context-free grammar fuzzing. :)

Directed graph inputs

Once the trees have relationships between branches, we need to reconsider how we mutate and crossover these inputs. I would argue that most input formats which have been historically fuzzed are directed (but acyclic) graph inputs: length fields which directly affect the length of the next segment, type fields which determine how they are parsed, variable definition and use relationships, etc.

When crossover or mutation on these input formats occur, we need to "rewire" the references to other branches which would otherwise be invalidated. Curiously, this weakness is also a strength: we can easily update which references these point to as a mutation.

Similarly, when we linearise these inputs (i.e., if our consumed input shape is actually a byte buffer), we get to choose the linearisation. Imagine an input for an interpreter like the following:

int f() {
  ...
}

int g() {
  ...
}

int h() {
  f();
  return g();
}

Because the constraint applied here is only that f and g must precede h, we can rewrite the input as such:

int g() {
  ...
}

int f() {
  ...
}

int h() {
  f();
  return g();
}

which results in an equivalent, but unequal input. In other words, for many of these input shapes, we get certain structural metamorphic relations [12] for free.

One could imagine doing something similar with e.g. assembly instructions where we realign jump targets. Provided that we know the order in which these instructions are executed, we can even do snapshot fuzzing based on execution trace, where (as long as we leave those "input" regions unmodified) we can update the instructions which have not yet been executed.

Beyond input shape cleverness

It is clear that there are different implications of different input shapes from the perspective of how we mutate these inputs, and the certain advantages they lend to the fuzzing campaign itself. In some circumstances, we can take advantage of the differences in these input formats on the same program.

Last year, Nick Wellnhofer implemented a new fuzzer for libxml2 [13]. This fuzzer, instead of parsing an existing XML tree produced by fuzzing, consumes the input as sequences of API calls. Beyond the simple implications of different APIs being tested, there was another advantage: the input shape changed from a directed graph to a linear input format.

Let's consider this briefly from a theoretical perspective. The two fuzzers target (approximately) the same program space, but access that program space by two different projections: the graph-like data input, which is consumed directly, and the linear instruction input, which is consumed one segment at a time and explores the program space by mutating the underlying state. There are stark differences between the two, but I would argue that both representations serve a purpose: the parsing fuzzer might provide inputs simply not constructable via API, and the API fuzzer will likely hit API functions that would have otherwise been missed by a simple parser fuzzer.

Even more critically, there is an opportunity here: to embrace the advantages of both input formats. Because the XML document being accessed via API operations can be serialised and unserialised, we may utilise a very simple snapshotting mechanism (i.e. simply serialising the document) and begin snapshot fuzzing with this newfound linear input shape. In other words, we may "start" the API fuzzer from a "snapshot" obtained by traditional fuzzing of the XML tree itself. Similarly, in the graph representation, we may replace cross-references according to information we can mine from the deserialisation process.

That being said, a cursory look at the harness [14] indicates that it is highly susceptible to data reinterpretation issues. Perhaps someone with a bit more time than I have presently could implement a custom mutator, or try fuzzing it with FrameShift [4]?

I imagine that there are many more targets we can do this with. Perhaps the next advance in fuzzing will not come from harness generation where we try to do the same as we've always done, but by fundamental reframing of the input space of our target programs.

A final note

It's very easy to fuzz parking puzzles with a linear instruction input shape, but the corpus explodes rapidly without a smart guidance mechanism. A similar story is true for Sokoban puzzles [7], where there are theoretical limitations on how smart we can become with our guidance [15]. Eventually, I think the story stays the same for the software that we test: there are hard theoretical limitations on how much guidance we can actually give our fuzzers, especially when we have very large state spaces to explore and not a whole lot to distinguish them with.

In some ways, this is quite reminiscent of the conclusion of Google Project Zero's recent post on exploiting Chromium with Unix socket bugs [16]. Some of these bugs are "obvious" when we look at the sequences which ended up triggering these bugs in the end. But just how much CPU power do we waste because of limited guidance, or because of oversensitive guidance? Reconsidering the input shape alone will not save us; fuzzing is just another tool in the bag and changing input shapes allows us to use that tool more effectively, but it is not the be-all-end-all of security testing.

Hopefully, as more research to understand the relationship between guidance strategies and input formats is completed, we will better understand the limits of fuzzing and navigate those gaps with other strategies. For now, though, this is a very promising next step that I hope you will consider for your next fuzzing campaign.